This question was posed to a class of pre-service teachers at the Graduate School of Education, Rutgers University, New Brunswick.
One student volunteered an answer of 16 1/2, which prompted questions from the class of where the “1/2” came from.
The student who volunteered the answer went to the board to explain, stating she would answer “how many 2/11 in 1?” first
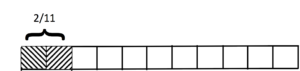
She drew a bar to represent the unit 1 and divided it into 11 pieces, which, she explained, we should take to be equal pieces:
![]()
She then shaded 2 adjacent pieces which she described as “2/11 of the bar”:
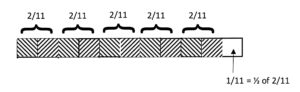
She then repeated this shading, counting 5 lots of “2/11” in total, with a remainder of “1/11”.
She then compared this remainder to the “2/11” she was repeating and said it was half of that, so, she said, there are 5 1/2 lots of 2/11 in 1:
Several students seemed surprised, and taken, by the explanation of where the “1/2” came from – that it was one half of the repeated unit of 2/11.
Not only was the presenting student’s brain awake to the ideas of a repeated unit and comparison of a remainder with that unit, but her presentation also seemed to awaken other students to the same round of ideas.
Is the thinking of the students in the communication, as a commcognitive point of view might assert, or is the thinking about repeated units and comparisons with that unit, in a non-language part of the brain that is simulated by, but not identical with, the written and spoken communication?
