Proof

One may ask where does a proof live: on paper, or in the heads of individual students of mathematics?

By “students” here we include professional mathematicians, who, of course, are always learning from others.

There is, of course, no definitive answer to this question. Some will aver that it is only when an argument is written down and inspectable by others that it might even be considered as a proof. Whereas, others will argue that the essence of a proof, including the essential insights that lead to the proof, live in individual brains, and that a written proof is no more than a linguistic representation of a proof in the brain.

This latter position can be represented in cartoon form, as similar to  a group of people who see what appear to be animal tracks on the ground, and one of them says: “Ah! A chicken.” The person is seeing not a chicken, of course, but the tracks left by a chicken.

(with apologies to Magritte).

So, the argument goes, the written record of a proof from an individual brain, or collection of individual brains, is not the proof after all, but just the record of a proof left by mathematicians: the proof lives in their brains and the written documents are a secondary record of that proof – a linguistic communication of the proof, not the proof itself.

Of course this is an undecidable issue, since we do not have a definition of what constitutes a proof.

On the face of it, Thurston seems to come down on the side of the idea that proofs really exist in individual brains and the written documents are secondary:

“Mathematical knowledge and understanding were embedded in the minds and in the social fabric of the community of people thinking about a particular topic. This knowledge was supported by written documents, but the written documents were not really primary.” 

A diagram such as the following:

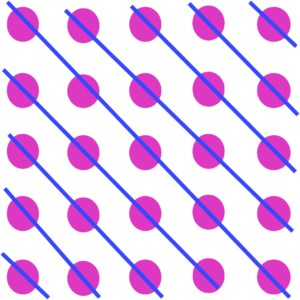
which is intended to communicate an insight, is not, by anyone’s standards, a proof that . Yet the idea for the more general diagram is already present in this particular diagram and, as James Tanton has written: “the epiphany of seeing those diagonals in the square array is a mathematical mind-awakening moment.”

Grothendieck was very clear about the primacy of the insight over proof:

“What my experience of mathematical work has taught me again and again, is that the proof always springs from the insight, and not the other way round – and that the insight itself has its source, first and foremost, in a delicate and obstinate feeling of the relevant entities and concepts and their mutual relations.”