“This might be crazy, but …”

Nineteen preservice elementary teachers, taught in Fall 2000, all underwent a substantial change in their views of mathematics. The principal agent for this change was the focus on building connections between different representations of a single problem, involving binary choice:

How many towers of height 4 can be made from blocks of 2 colors? How many towers of height 5?
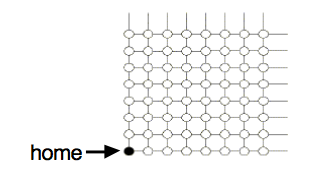
On the grid shown below, indicate on each dot how many different ways there are to walk to that dot from “home” given that you can only walk UP or RIGHT.

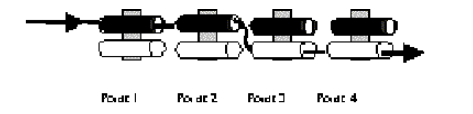
Portion of an integer lattice on which students performed walks UP or RIGHT from “home” to horizontally or vertically adjacent dots

How many different ways are there to run through a series of 4 tunnels if you must pass through exactly two white and two black tunnels? At each point, the runner goes through only a black or white tunnel.

At each point, the runner goes through only a black or white tunnel

$(a + b)^2 = a^2 + 2ab + b^2$ . What are the corresponding expansions for $(a + b)^3$ and $(a + b)^4$ ?

The problems we chose were unlikely to allow a solution by a remembered formula.

One student speculated during class that there might be a connection between towers, grid walks and binomial expansions. He gave an explanation in class, prefaced by a statement along the lines: “This might be crazy, but I think…” that $(a + b)^2 = a^2 + 2ab + b^2$ could be interpreted as saying something about block towers and grid walks. Namely, if a and b were interpreted as two colors, the binomial expansion says there is 1 tower of height two built from the “a” color, 1 from the “b” color, and 2 using both the “a” and “b” colors. The student used black (B) and white (W) and wrote the binomial expansion as $(B + W)^2 = B^2 + 2BW + B^2$ . He then interpreted the same expression in terms of grid walks by taking B to mean “walk UP” and W to mean “walk RIGHT”. Finally, he related towers and grid walks to the other binomial expansions, and the patterns of numbers on the grid to Pascal’s triangle. The atmosphere following this student’s presentation to the class was electric. The other students gave him a spontaneous round of applause and he, with four other students, stayed for an hour after class exploring these connections. This episode was etched into the memory of many of the students, as student write-ups and reflections show:

“If you go through the tunnel with the pattern of BWBW, you can also make a tower of BWBW. If you think of B as equalling right and W as equalling up, you can go RURU. Algebraically, you can replace the a and b with a B and W and have (B+W) raised to whichever high, which I’m using 4. It shows $(B+W)^4 =B^4+4B^3W+6B^2W^2 +4BW^3 +W^4$ . If you add up all the numbers in front, you get the number of possibilities. The exponents are the number of the different colors you have. Ex: $4B^3W$ means there are 3 blacks and 1 white, with 4 different ways of arranging it. To have two of 2 of each like the tunnels ask, would be $6B^2W^2$ , which means there are 6 possibilities with 2 black and 2 white.” (Reflection, Week 4)

“… although I used Pascal’s triangle many times throughout high school, I never truly understood why it worked. By completing the grid walk exercises, so many things have become clear to me. Well, I learned the secret of the grid walks and of Pascal’s Triangle…. I really wish I had known this when I was in Algebra. All we were taught then was that, for some reason unknown to me and probably many others in the class, the rows of Pascal’s Triangle made up the coefficients in binomial expansion. Now I not only understand how to use the triangle algebraically, I know why it works. The numbers in an algebraic expression along with the variables can represent different groups of objects, in a manner of speaking. It all makes sense. This simple understanding, but by no means easy, is so rewarding because the knowledge has become my own. And I know that ten years from now, I will still be able to explain this problem.” (End-of-semester write-up, week 16)

Samples of reflective writing of a student in the class.
McGowen, M.A. & Davis, G.E. (2001) Changing Pre-Service Elementary Teachers’ Attitudes to Algebra. In H. Chick, K. Stacey, J. Vincent & J. Vincent (Eds.) The Future of the Teaching and Learning of Algebra. Proceedings of the 12th ICMI Algebra Study Conference. Melbourne, Australia: The University of Melbourne.

“This might be crazy, but …”

Direct Your Visitors to a Clear Action at the Bottom of the Page